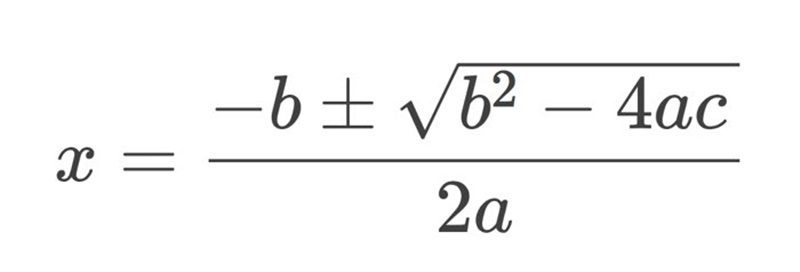Na světě se však najde pár matematických géniů, kteří mají matematiku takříkajíc v krvi. Patří mezi ně i Po-Shen Loh, vědec, kterému se podařilo najít nové, zjednodušené řešení kvadratických rovnic.
Podaří se zjednodušit řešení kvadratických rovnic?
V průběhu základní a střední školy měl matematiku každý z nás, jistě jste se tedy i vy řešili kvadratické rovnice. Pokud však nejste fanouškem matematiky, je možné, že váš mozek tuto vzpomínku potlačil a víte akorát to, že kvadratické rovnice existují. Mezi matematické génie patří i vědec jménem Po-Shen Loh z Univerzity Carnegie Mellon.
Jak uvádí portál ScienceAlert, právě jemu se podařilo odhalit nové, jednodušší řešení kvadratických rovnic, na které se nikomu nepodařilo přijít tisíce let. Ve své studii Loh tvrdí, že kvadratická rovnice je jedním z největších triumfů matematiky a její původ sahá až do dob Babylonské říše. I to je jeden z důvodů, proč se ji již od nepaměti učí miliardy lidí po celém světě v rámci povinného vyučování matematiky.
Kvadratické rovnice z dob Babylonské říše
Zdá se však, že memorování vzorce, který se používal tisíce let, již dále nebude nezbytné. Samozřejmě i v současnosti existuje několik možností, jak kvadratickou rovnici upravit, jako například řešení kvadratické rovnice za pomoci diskriminantu. Častou a při jednodušších kvadratických rovnicích častěji používanou metodou, je rozložení rovnice na součin či úprava na čtverec.
Základní vzorec pro výpočet kvadratické rovnice za pomoci diskriminantu vypadá takto:
Všeobecný tvar kvadratické rovnice: ax2 + bx + c = 0
Nové řešení, na které Loh přišel zcela náhodně při brainstormingu, je údajně jednodušší, efektivnější a mnohem snadněji zapamatovatelné. Loh zůstal z objevu šokován a říká, že nerozumí, jak je možné, že na toto řešení dosud nikdo nepřišel. Loh vychází ze základního předpisu ax² + bx + c = 0, přičemž existují dvě řešení této rovnice. V rámci prvního z nich se spoléháme na rozklad vzorce na součin ve tvaru (x -) (x -). Zde hledáme dvě čísla zapadající na prázdná místa. Součet dvou čísel by přitom měl být rovný b a součin zas c. Pokud toto řešení selže, hledáme řešení za pomoci diskriminantů, tedy za pomoci vzorce.
Na nové řešení se přišlo po tisíciletích
Loh ve svém příspěvku popisuje různá řešení kvadratické rovnice x2 – 2x – 24 = 0 přidává i svou novou metodu, kterou nazývá faktorizace bez hádání. V ní využívá techniku průměrování, přičemž se zaměřuje na součet. Dosud využívaná technika se zaměřovala na součin dvou čísel, jejichž výsledkem by bylo c (v tomto případě 24). Jak uvádí Loh, součet dvou čísel je 2, zatímco jejich průměr je 1. Můžeme tedy hledat čísla, která se rovnají 1 plus nějaké množství a 1 minus stejné množství. Označme to „nějaké množství“ písmenem u. Pak by to znamenalo, že hledáme číslo, které by splňovalo předešlé podmínky, tedy 1 + u a 1-u, přičemž u může být i 0.
Platí, že součin našich hledaných kořenů musí být rovný c, tedy, že (1 + u) (1-u) = – 24. Úpravou této rovnice získáváme opět rovnici kvadratickou, tentokrát však mnohem jednodušší 1 – u2 = – 24. Z této rovnice již víme jednoduše určit, že u je 5 nebo – 5, stačí když v dalších výpočtech využijeme jeden tvar, výsledek je vždy stejný. Vzpomeneme si totiž na rovnici (1 + u) (1 – u) = 24 a zjistíme, že námi hledané kořeny jsou tedy 6 (1 + u = 1 + 5 = 6) a – 4 (1 – u = 1 – 5 = – 4).
Hledání zmíněného u je podle Loha intuitivní a jednodušší, než kdybychom měli hledat dvě čísla patřící do závorek (x-) (x -).
Loh dodává, že podobná práce, jako ta jeho, byla publikována ještě v roce 1989, její autor však nedošel k zjednodušenému závěru, jen k němu směřoval. Pokud se Lohové podezření, že s řešením dosud nikdo nepřišel, potvrdí, je možné, že se brzy budou přepisovat učebnice matematiky.